[最新] y=a(1+r)^t what is a 309210-Y1 technology app
As shown in the plot at the right = k in 10 −4 cm 3 mol −1 s −1 T in K Substituting for the quotient in the exponent of E a / R = 12,667 K approximate value for R = 1446 J K −1 mol −1 The activation energy of this reaction from these data is thenThe general equation for depreciation is given by y = A(1 – r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was purchased 6 years ago for $25,000 If the annual Math The average monthly payment on a new car is $523 The interest on a car loan is $8469 a yearGoogle's free service instantly translates words, phrases, and web pages between English and over 100 other languages

Warmup Solve Log Ppt Download
Y1 technology app
Y1 technology app-I think you use the following formula y=a (1r)^t where y is the amount after t years, a is the initial amount, r is the annual growth rate, and t is the time in years I will appreciate everyonesR = 005 or 5% annual interest rate t = 3 years P = the principal A = the future value I = A P is the interest A = P(1 r)^t I = P(1 r)^t P I = P((1 r)^t 1) I = P((1 005)^3 1) I = P* He will earn P* dollars interest


Exponential Growth And Decay Examples Solutions Videos Worksheets Activities
Y = A(1 – r)^t (the ^ is an important distinction, meaning "to the power of" t, whereas as you have the equation written right now, it says "divided" by t) So these are the variables we know A =Let, y = a^x Taking logarithm on bothsideboth side ln(y)=x * ln(a) Differentiating both side wrt x d/dx{ln(y)} =d/dx{x*ln(a)} (1/y)dy/dx = x*0 ln(a)*1=ln(a) dy/dx = y*ln(a) = a^x * ln(a)In mathematics and its applications, the root mean square (RMS or rms) is defined as the square root of the mean square (the arithmetic mean of the squares of a set of numbers) The RMS is also known as the quadratic mean and is a particular case of the generalized mean with exponent 2 RMS can also be defined for a continuously varying function in terms of an integral of the squares of the
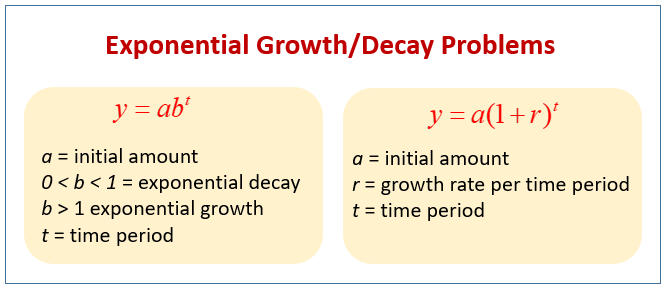
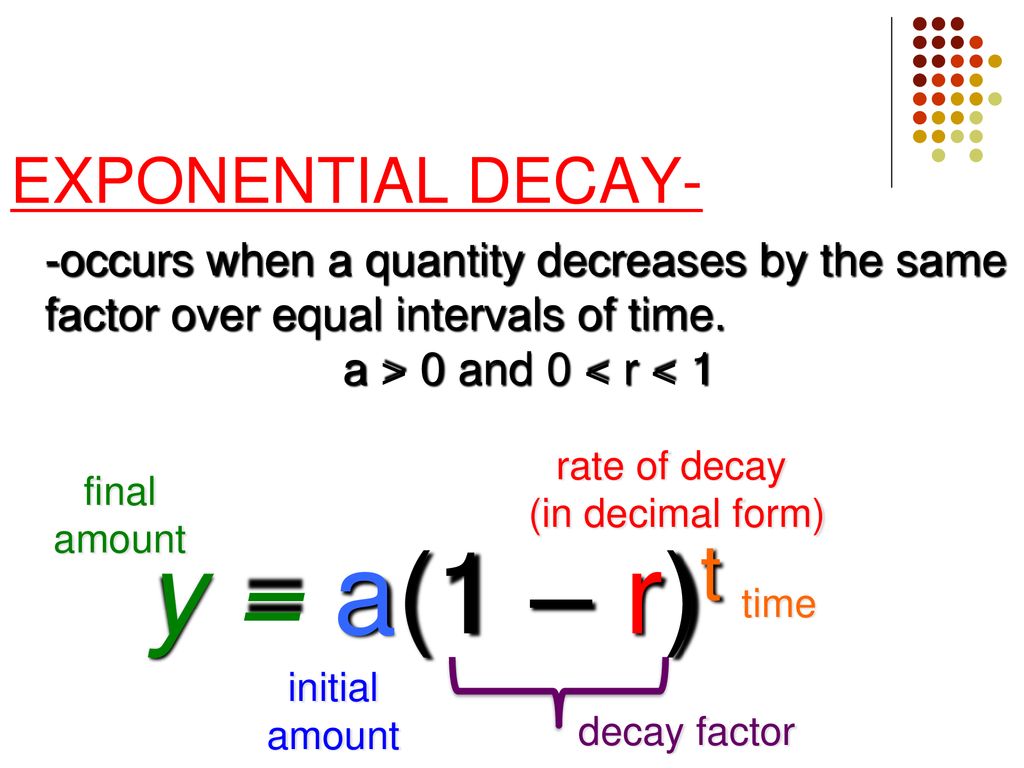
A quantity is decreasing exponentially if it decreases by the same percent in each time period C is the initial amount t is the time period (1 – r ) is the decay factor, r is the decay rate The percent of decrease is 100 r y = C (1 – r ) t W RITING E XPONENTIAL D ECAY M ODELS E XPONENTIAL D ECAY M ODEL 9Answer to An equation for the depreciation of a car is given by y = A(1 r)^{t}, where y = current value of the car, A = original cost, r = rateWhen x is a vector, it is treated as a column, ie, the result is a 1row matrix Value A matrix, with dim and dimnames constructed appropriately from those of x, and other attributes except names copied across Note The conjugate transpose of a complex matrix \(A\), denoted \(A^H\) or \(A^*\), is computed as Conj(t(A))
Solve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponentSolve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponentY = a(1 r)t Write exponential growth model = 609(1 )t Substitute 609 for a and for r = 609()t Simplify Using this model, you can estimate the world population in 05 (t = 5) to be y = 609()5 ≈ 646 billion b Use the table feature of a graphing calculator to determine that y ≈ 7 when t = 12 So, the world population was about 7 billion in 12



8 8 Exponential Growth Decay



Ppt 8 1 8 2 Exponential Growth Decay Powerpoint Presentation Free Download Id
An equation for the depreciation of a car is given by y = A (1 r)^ {t}, where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a carIV ( Points) Consider r(t) 1R' such that the curve of r(t) is of torsion 7 0 We consider also that the curve lies on a sphere centered at the origin and of radius R and that it verifies Vol = 1 We call these curves spherical curves We denote by k its curvature, r its torsion, Tits unit tangent, N its principal unit normal and B itsA)33 years B)50 years C)56 years D)66 years


Http Www Ozark K12 Mo Us Cms Lib011 Mo Centricity Domain 533 Doc Pdf



Exponential Growth And Interest
Ln ( k ) = ln ( A ) − E a R ( 1 T ) {\displaystyle \ln (k)=\ln (A) {\frac {E_ {a}} {R}}\left ( {\frac {1} {T}}\right)} When plotted in the manner described above, the value of the yintercept (at x = 1 / T = 0 {\displaystyle x=1/T=0} ) will correspond to ln ( A ) {\displaystyle \ln (A)}Exponential Growth of the Form y = a(1 r)t In 1910, the population of a city was 1,000 Since then, the population has increased by exactly 15% per year If the population continues to grow at this rate, what will the population be in 10?Hence, r = 1 = , or, rounding the value of "r" to the nearest tenthousandth, r = 0630 Therefore, your answer is y = 5*()^t It is EXACTLY the form you requested, with the value of r = 0630, rounded as it is assigned by the problem



Rate Of Decay Youtube


Http Www Mtsd K12 Nj Us Cms Lib5 Nj Centricity Domain 378 4 1 4 2 packet answers Pdf
(b) Determine the matrix of T with respect to the standard bases of P 2(R) and R2 Solution First we recall that the standard basis of P 2(R) is β = {1,x,x2} and that the standard basis of R2 is γ = {(1,0),(0,1)} Now we look at the image of eachP 0 = initial amount at time t = 0 r = the growth rate as a percentage (1% = 001) t = time – the number of periods (intervals) This could be months or years – just depends on when the rate compounds This form is solving for P(t), or the future value You can also shift this formula around and solve for any other variable!Learn termexponentialgrowth = y=a(1r)^t with free interactive flashcards Choose from 500 different sets of termexponentialgrowth = y=a(1r)^t flashcards on Quizlet



Ppt 8 8 Exponential Growth Decay Powerpoint Presentation Free Download Id


Q Tbn And9gcqijosvjs X3b0gges Uh2g7tqf4q8ek Jt2uxlutl7txidqktm Usqp Cau
P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the givenA)33 years B)50 years C)56 years D)66 yearsThe infix operator %>% is not part of base R, but is in fact defined by the package magrittr and is heavily used by dplyr () It works like a pipe, hence the reference to Magritte's famous painting The Treachery of Images What the function does is to pass the left hand side of the operator to the first argument of the right hand side of the operator



Essential Skills Solve Problems Involving Exponential Growth Solve Problems Involving Exponential Decay Ppt Download



Exponential Growth Decay Ppt Download
Using the given equation y = A (1 – r)^t you can calculate the car current value y = * (1 015)⁴ = * 085⁴ y = $12, answered itscheesycheedar $12, Stepbystep explanation Given The original value of car = $24,000 The rate of depreciation = 15%=015# A formula y ~ x # A converted formula y = a_1 a_2 * x This is an example of a simple conversion y ~ x gets translated into y = a_1 a_2 * x To see and understand what R actually happens, you can use the model_matrix() function This function creates a design or model matrix by, for example, expanding factors to a set of dummy variables, depending on the contrasts, and expanding interactions similarlyR = rate (% in decimal form);


Do Now 1 22 19 Take Out Hw From Last Week Copy Hw In Your Planner Ppt Download
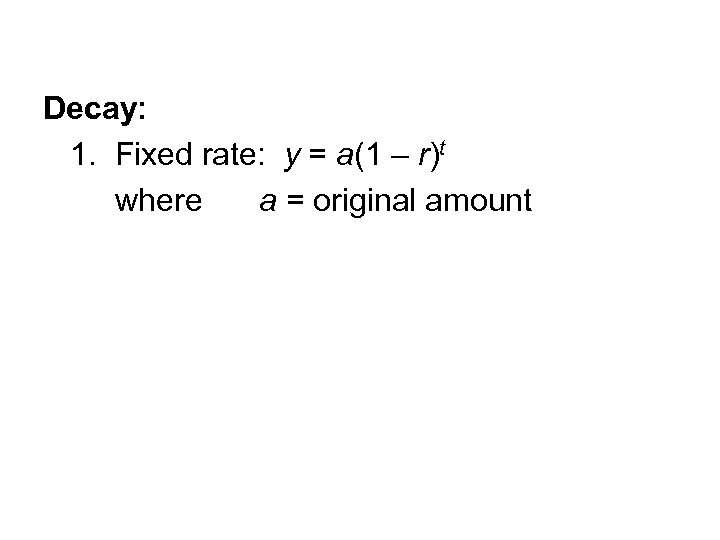


8 8 Exponential Growth Decay
Y = a(1 r)t EXPONETIAL DECAY FUNCTION y = a(1 – r )t EXPONENTIAL DECAY APPLICATIONS 5 The population of a town is 2500 and is decreasing at a rate of 35% per year Write an exponential decay function to find the population of the town after 5 years EXPONENTIAL GROWTH APPLICATIONS 11Find the tangent vector r′(t) at the point where t=2 given r(t)=(4cos(πt))i(2sin(πt))j(2t)k 2Give the vector parameterization of the tangent line to r(t)=(e t)i(e3t)j(3ln(t))k at the point where t=1 3Give the vector parameterization of the tangent line to r(t)=(4t 2)i(1−t)j(2t 2 2)k at the point P(4,0,4) 4Scalar parametric equations for the line tangent to the graph ofIn a labatory, a culture increases from 30 to 195 organisms in 5 hours What is the hourly growth rate in the growth formula y=a(1r)^t y=a(1r)^t The problem gives us y as 195 a as 30 t as 5 195=30(1r)^5 195/30 = (1r)^5 65 = (1r)^5 65^(1/5) = 1r 65^(2) = 1r 65^(2) 1 = r 1454 1 = r 0454 = r 454% = r


Www Webassign Net Latex2pdf 08e98e804afc0ea8670e500bf2b0 Pdf


Http Melaniewingard Weebly Com Uploads 3 7 5 5 01 24 17 Section 6 1 Exponential Growth And Decay Pdf
Y = a(1 r)t Write exponential growth model = 609(1 )t Substitute 609 for a and for r = 609()t Simplify Using this model, you can estimate the world population in 05 (t = 5) to be y = 609()5 ≈ 646 billion b Use the table feature of a graphing calculator to determine that y ≈ 7 when t = 12 So, the world population was about 7 billion in 121Find the tangent vector r′(t) at the point where t=2 given r(t)=(4cos(πt))i(2sin(πt))j(2t)k 2Give the vector parameterization of the tangent line to r(t)=(e t)i(e3t)j(3ln(t))k at the point where t=1 3Give the vector parameterization of the tangent line to r(t)=(4t 2)i(1−t)j(2t 2 2)k at the point P(4,0,4) 4Scalar parametric equations for the line tangent to the graph ofExponential growth of the Form y = aekt


Mrsjblanco Weebly Com Uploads 5 3 6 1 Growth And Decay Power Point Pdf


Http Www Peoriapublicschools Org Cms Lib2 Il Centricity Domain 1464 8th jan 18 Pdf
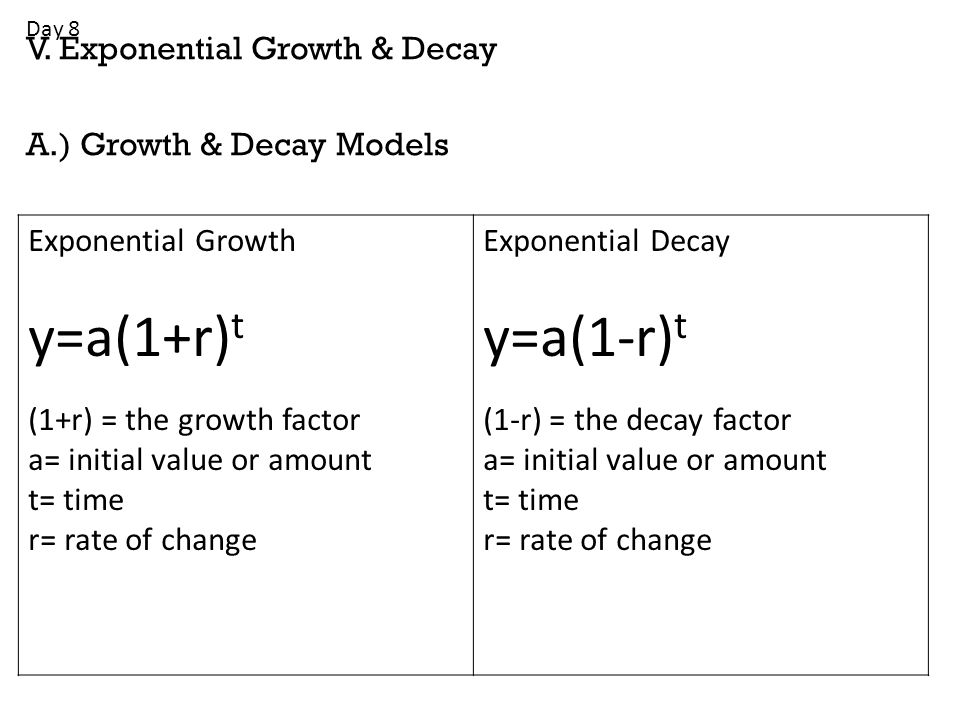
T = time periods Write an exponential function to model each situation Find each amount at the end of the specified time Round your answers to the nearest whole number 1 A town with a population of 5,000 grows 3% per yearA L I F I Y A ' S A R T, Mumbai, Maharashtra 239 likes · 1 talking about this Art Logo Design Illustrations Packaging Branding Typography Geometry UI/UX Mural Design CommunicationA function of the form y=a(1 r)t, where a> 0 and r> 0, is an exponential growth function initial amount time growth factor rate of growth (in decimal form) final amounty=a(1 r)t WWhat You Will Learnhat You Will Learn Use and identify exponential growth and decay functions Interpret and rewrite exponential growth and decay functions



Solved Chemistry After 12 Hours Half Of A 16 Gram Sample Chegg Com


Http Melaniewingard Weebly Com Uploads 3 7 5 5 03 17 17 Sections 8 1 8 2 Part 3 Exponential Growth And Decay Word Problems Pdf
Y = a(1 r)t EXPONETIAL DECAY FUNCTION y = a(1 – r )t EXPONENTIAL DECAY APPLICATIONS 5 The population of a town is 2500 and is decreasing at a rate of 35% per year Write an exponential decay function to find the population of the town after 5 years EXPONENTIAL GROWTH APPLICATIONS 1An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?Solve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponent



Maths Sci 12 व Pages 51 100 Flip Pdf Download Fliphtml5


Www Marsd Org Cms Lib Nj Centricity Domain 8 6 1 6 2 review key Pdf
P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the givenUsing the growth formula we have y = a(1 r) x where a = 1 (we start with 1 bacteria), and r = 100%, since the amount doubles y = 1(1 100) x = 2 x (same result) Notice that the graph is a scatter plot You cannot have a fractional part of a bacteria The dotted line is the exponential function which contains the scatter plots (the model)Exponential Word Problems Growth & Decay Growth Formula y = a (1 r) t Decay Formula y = a (1 – r) t where a = original number;


Solucionarioecuacionesdiferencialesdenniszill7aedicion P


Http Www Cbsd Org Cms Lib Pa Centricity Domain 17 8 1 8 2 exponential growth and decay key Pdf
Question An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?I was reading the documentation on R Formula, and trying to figure out how to work with depmix (from the depmixS4 package) Now, in the documentation of depmixS4, sample formula tends to be something like y ~ 1For simple case like y ~ x, it is defining a relationship between input x and output y, so I get that it is similar to y = a * x b, where a is the slope, and b is the interceptAn equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?



Summarise The With R And Rgl R Bloggers



Chapter 10 Binary Trees X Y A B
Answers 1 Show answers Another question on Mathematics Mathematics, 10 Can someone check if i did this right since i really want to make sure it's correct if you do you so much Answers 1 Answer Mathematics, 1930The formula I'm using is $y = a (1r)^t$, with a being the initial amount, $r$ being the rate in decimal form, and $t$ is time relative to the rate, which makes $y = 3,750(106)^{132}$ How do I solve for the ending amount ($y$)?# A formula y ~ x # A converted formula y = a_1 a_2 * x This is an example of a simple conversion y ~ x gets translated into y = a_1 a_2 * x To see and understand what R actually happens, you can use the model_matrix() function This function creates a design or model matrix by, for example, expanding factors to a set of dummy variables


Www Humbleisd Net Cms Lib Tx Centricity Domain 35 Section 4 6 exercises Pdf


Mrsjblanco Weebly Com Uploads 5 3 6 1 Growth And Decay Power Point Pdf
R = rate of growth or decay, and t = time Exponential growth y = a (1 r)t Exponential decay y = a (1 − r)t The population of a city is increasing at a rate of 4% each year In 00, there were 236,000 people in the city Write an exponential growth function to model this situation Then find the population in 09 Step 1 Identify the variablesY = a(05) t/x represents the amount y of a substance remaining after t years, where a is the initial amount and x is the length of the halflife (in years) Plutonium238 Halflife years a A scientist is studying a 3gram sample Write a function that represents the amount y of plutonium238 after t years bLn ( k ) = ln ( A ) − E a R ( 1 T ) {\displaystyle \ln (k)=\ln (A) {\frac {E_ {a}} {R}}\left ( {\frac {1} {T}}\right)} When plotted in the manner described above, the value of the yintercept (at x = 1 / T = 0 {\displaystyle x=1/T=0} ) will correspond to ln ( A ) {\displaystyle \ln (A)}



Exponential Growth And Decay



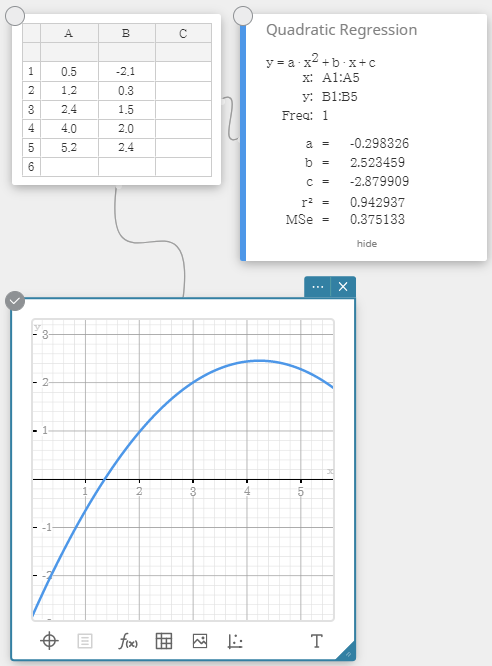
The Regression Equation Introduction To Statistics
What is the decay factor in the exponential decay function y=a(1−r)t ?A L I F I Y A ' S A R T, Mumbai, Maharashtra 239 likes · 1 talking about this Art Logo Design Illustrations Packaging Branding Typography Geometry UI/UX Mural Design Communication


Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Hw 80 key 9h Pdf



R Markdown Inline Latex Equations Vs Stack Overflow



Exponential Growth And Decay By Shaikha Arif Grade 10 Mrs Fatma Ppt Download


Http Www Mpsaz Org Rmhs Staff Esritter Algebra2 Files 6 1 6 4 Review Key Pdf



Warm Up Solve For X Log Ppt Download


Exponential Decay And Growth Home



Objectives Understand The Exponential Growth Decay Function Family Graph Exponential Growth Decay Functions Use Exponential Functions To Model Ppt Download


Www Wappingersschools Org Cms Lib Ny Centricity Domain 848 1 3 6 4 day 1 growth and decay Pdf


Www Strongnet Org Cms Lib Oh Centricity Domain 990 9 3 guided notes key Pdf



Make A Scatter Plot Of The Data In The Table Given Chegg Com



Solved Determine Whether The Following Curve Uses Arc Len Chegg Com



Warmup Solve Log Ppt Download
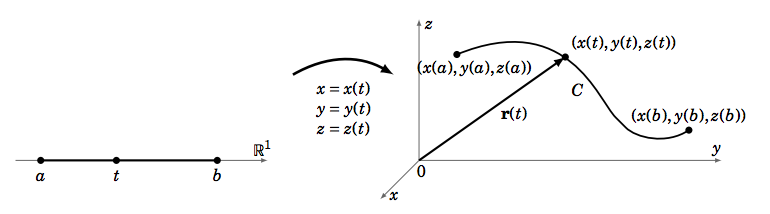


4 4 Surface Integrals And The Divergence Theorem Mathematics Libretexts



Exponential Growth And Decay



A Sin T Tcost Tant 8 At Any Point T On The Curve X A



7 1 Exponential Functions Ppt Video Online Download



Solved 2 Assume A Closed Smooth Curve Y A B R2 Chegg Com



Exponential Growth And Decay By Shaikha Arif Grade 10 Mrs Fatma Ppt Download



Exponential Growth And Decay Youtube


If X A 8 Sin8 Y A 1 Cos8 Find D 2y Dx 2 Sarthaks Econnect Largest Online Education Community


Prince Bubblegum St 12 Algebra 2 Adventure Time


A18 9 Exponential Decay Example Youtube


The Helen Of Geometry Explore Cycloids Najia Bao Good Morning Everyone Today Let S Investigate And Explore The Helen Of Geometry That Is Cycloid It Was The First Time That I Heard About Cycloid When I Was 12 Years Old My Father A Mechanical
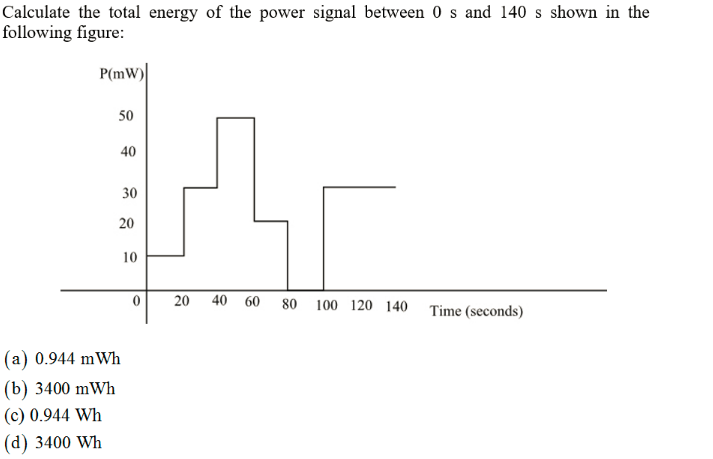


Solved Consider The Following Equations For Y D And D Y T Chegg Com
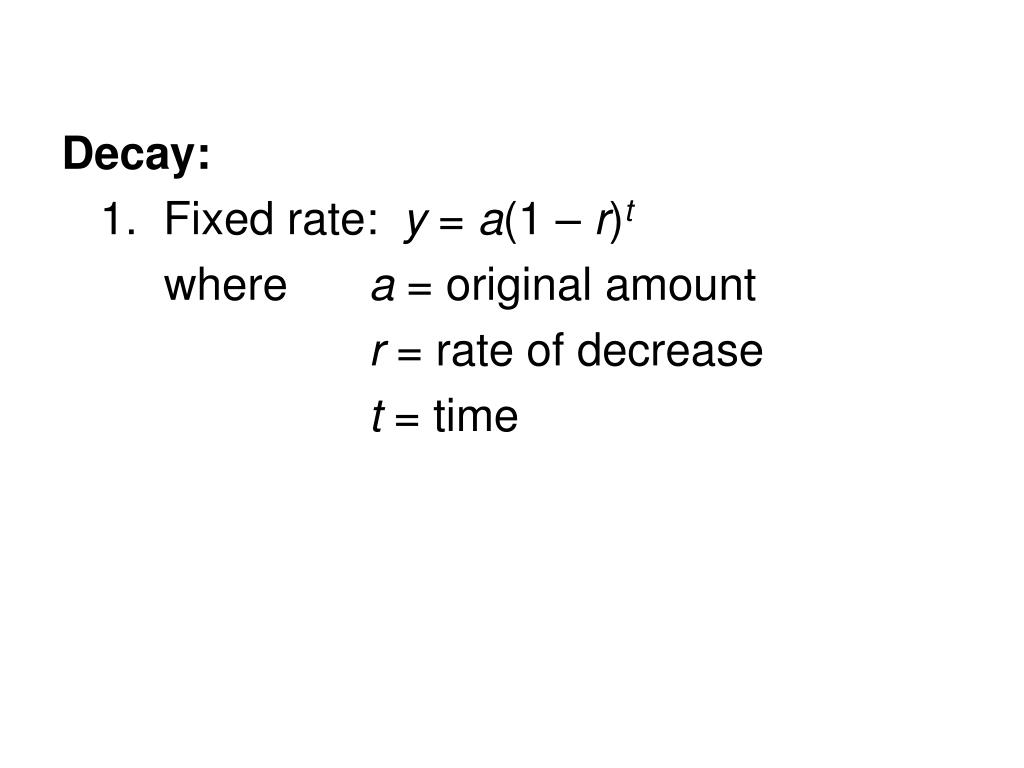


Ppt 8 8 Exponential Growth Decay Powerpoint Presentation Free Download Id



Exponential Growth And Decay Examples Solutions Videos Worksheets Activities


Www Cbsd Org Cms Lib Pa Centricity Domain 1906 Alg2 8 4 exponential growth and decay models pd 1 Pdf



Comparing Forms Of Exponential Functions Y Ab X And Y Ae Kx Youtube


Math 1010


Http Teachers Sheboygan K12 Wi Us Sdamrow Documents 106pdf Pdf


Www Wappingersschools Org Cms Lib Ny Centricity Domain 848 12 14 6 4 day 1 Pdf
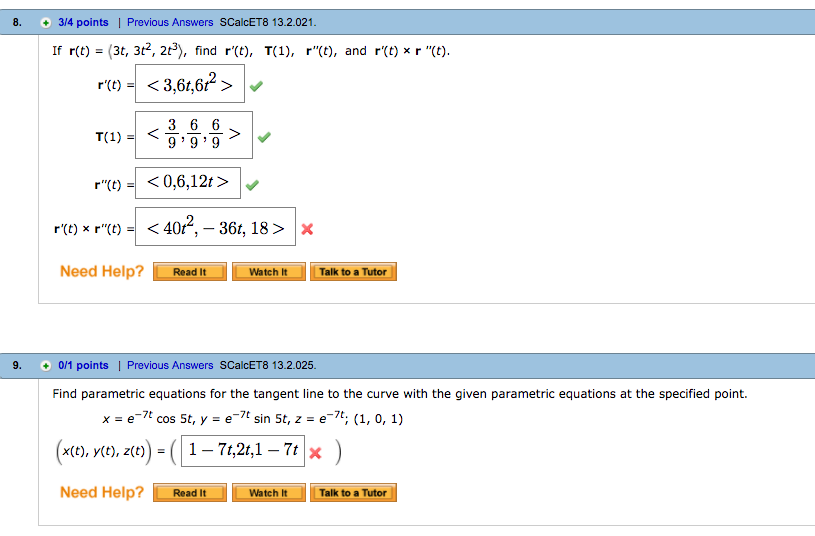


Solved If R T 3t 3t 2 2t 3 Find R T T 1 R T Chegg Com



Ex 9 3 3 Form Differential Equation Y A x B E 2x



8 8 Exponential Growth Decay



Solved 3 12 Thermistor Transfer Function The Transfer Fu Chegg Com



Chapter 7 Flashcards Quizlet



8 8 Exponential Growth Decay



Ppt 8 1 Exponential Growth 8 2 Exponential Decay Powerpoint Presentation Id



How To Find This Line Integral And What Is Its Answer Mathematics Stack Exchange


User Guide Classpad Net


L Earning T Arget 6d I Can Explain When A Situation Can Be Modeled By Exponential Growth Or Decay Solve The Problem And Interpret My Solution Within Ppt Download



Ppt Exponential Growth Decay Powerpoint Presentation Free Download Id


Q Tbn And9gctcmz1dsomdzqngkur Wtg8cte8xq9jfvcbbexja5xogjwzzi1m Usqp Cau
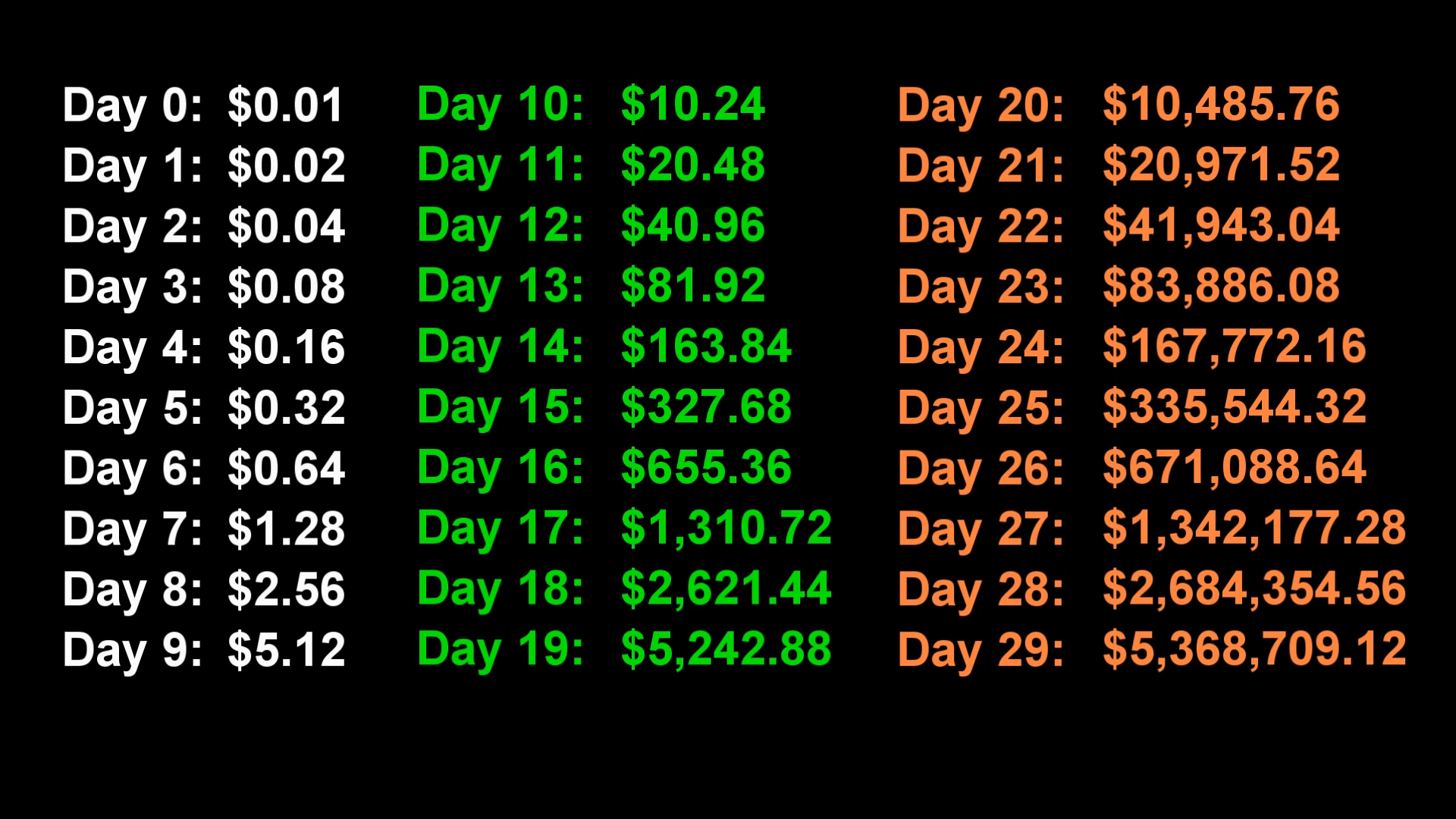


Dangers Of Exponential Growth Viruses And Atomic Bombs Yesil Science



Ppt 8 8 Exponential Growth Decay Powerpoint Presentation Free Download Id


Www Sccollege Edu Departments Math Documents Math 140 05 04 0 Pdf
.14_4247565755675833184.png)


If X A Cost Log Tan T 2 Y A 1 Sint Find D2y Dx2 Math Differential Equations Meritnation Com


Www Wsfcs K12 Nc Us Cms Lib Nc Centricity Domain 1499 Growth and decay student notes Pdf
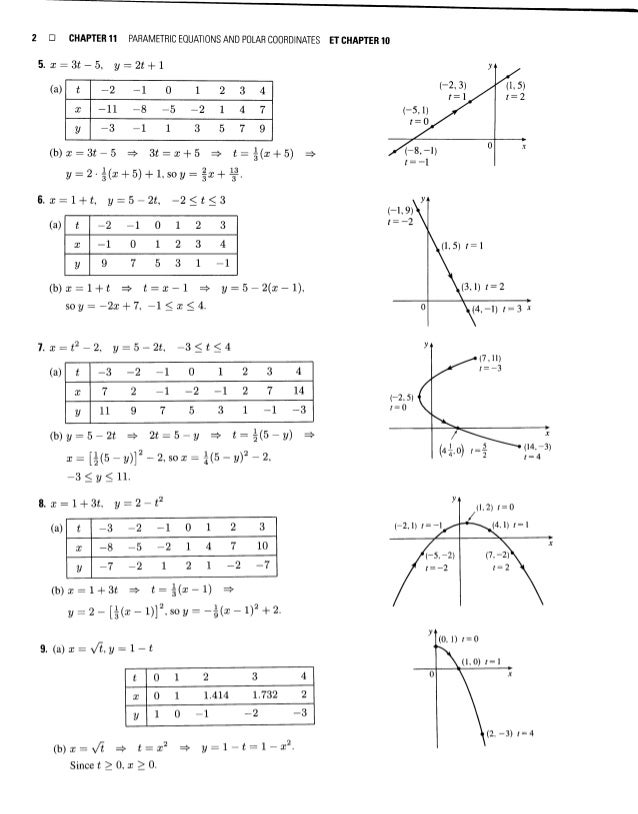


10 Parametric Equations 26 Polar Coordinates



Parameterization And Vector Fields 17 1 Parameterized Curves



Graph Y B For 0 B 1 Ppt Video Online Download


Www Scarsdaleschools K12 Ny Us Cms Lib5 Ny Centricity Domain 360 Exponentialgrowthdecay Pdf


Q Tbn And9gcsf Clj0ynqwjzduogv4wdkccija92j8h8vzpxuucmui5delfy5 Usqp Cau



Obfuscated Hello World Program
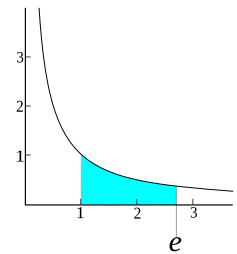


E Mathematical Constant Wikipedia



Solved Consider The Following Equations For Y D And D Y T Chegg Com



8 8 Exponential Growth Decay


Exponential Growth And Decay Posters And Reference Sheets By Plan Teach Math



Calculus 2 Parametric Equations 18 Of Find The Area Of An Arch Of A Cycloid Youtube


4 2 Algebra 2 Study Site


Projecteuclid Org Download Pdf 1 Euclid Acta



Solved Creating A 2nd Order Function In Matlab Under The Chegg Com



Exponential Functions Flashcards Quizlet



8 8 Exponential Growth Decay



Calculus 2 Parametric Equations 17 Of Find The Slope Of A Cycloid Youtube


Www Math Ucla Edu Vsv Liegroups07 7 Pdf



Graph Exponential Growth Functions Ppt Video Online Download



8 8 Exponential Growth Decay


Www Crsd Org Cms Lib Pa Centricity Domain 386 Section 7 1 day 3 notes key Pdf



Math 1525 Supplement Sheet For Lab 3



Ps02 Cmth03 Unit 1



Solved Bunter Was Asked To Solve The Following Maximizati Chegg Com



Exponential Functions Posters Reference Sheets Bundle Exponential Functions Word Problem Worksheets Exponential Growth
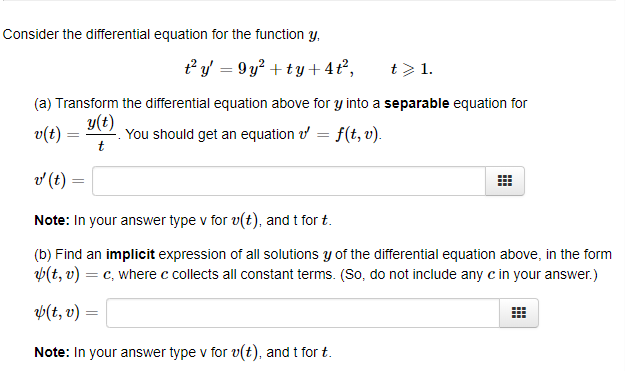


Solved Consider The Initial Value Problem For The Functio Chegg Com


Exponential Decay And Growth Home


Q Tbn And9gcqva6kwkjyd2rdsih05tmpg8ppumkliqmlp8mikzy1chqinh1dj Usqp Cau


コメント
コメントを投稿